INTERCEPT函数：求解直线与Y轴交点的数学技巧

利用现有的 x 值与 y 值计算直线与 y 轴的截距。

截距为穿过已知的 known_x's 和 known_y's 数据点的线性回归线与 y 轴的交点。

当自变量为 0（零）时，使用 INTERCEPT 函数可以决定因变量的值。

例如，当所有的数据点都是在室温或更高的温度下取得的，可以用 INTERCEPT 函数预测在 0°C 时金属的电阻。 

语法 
INTERCEPT(known_y's,known_x's) 

Known_y's 因变的观察值或数据的集合。 
Known_x's 自变的观察值或数据的集合。 

说明 

￭参数可以是数字，或者是包含数字的名称、数组或引用。

￭若数组或引用参数包含文本、逻辑值或空白单元格，则这些值将被忽略；但包含零值的单元格将计算在内。

￭若 known_y's 和 known_x's 所包含的数据点个数不相等或不包含任何数据点，则 INTERCEPT 返回错误值 #N/A。

￭其中 x 和 y 为样本平均数 AVERAGE(known_x's) 和 AVERAGE(known_y's)。 

INTERCEPT函数的作用是根据已知的坐标计算直线与Y轴的交点。

下面演示此函数的使用方法，帮助大家理解。

￭首先打开表格，将光标放在B9处。点击插入函数-统计-INTERCEPT函数。

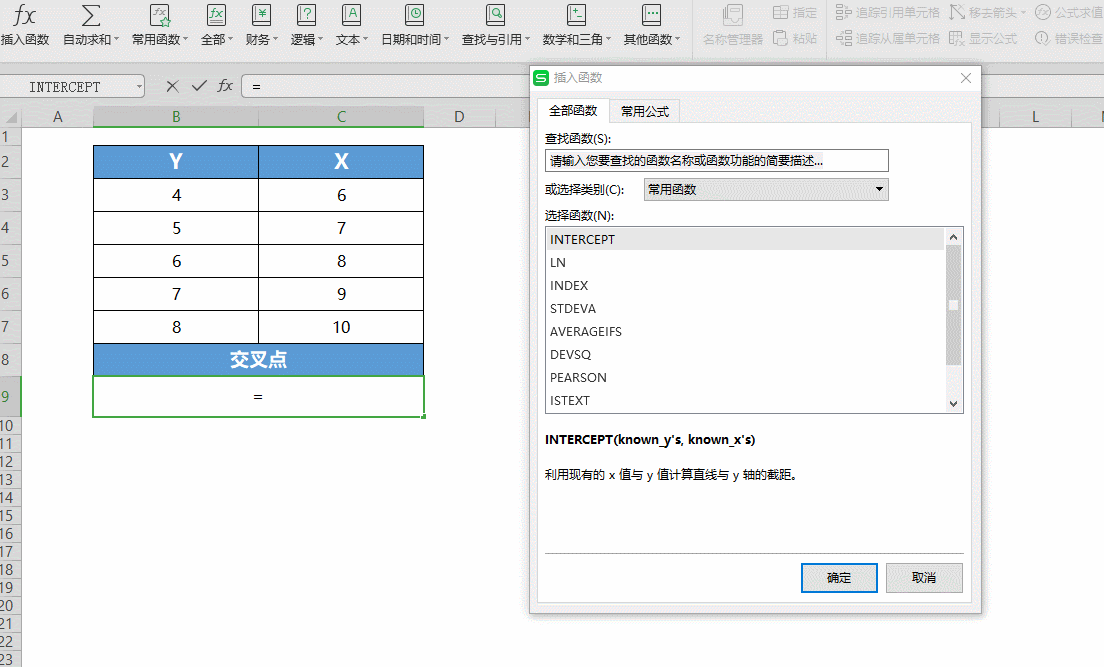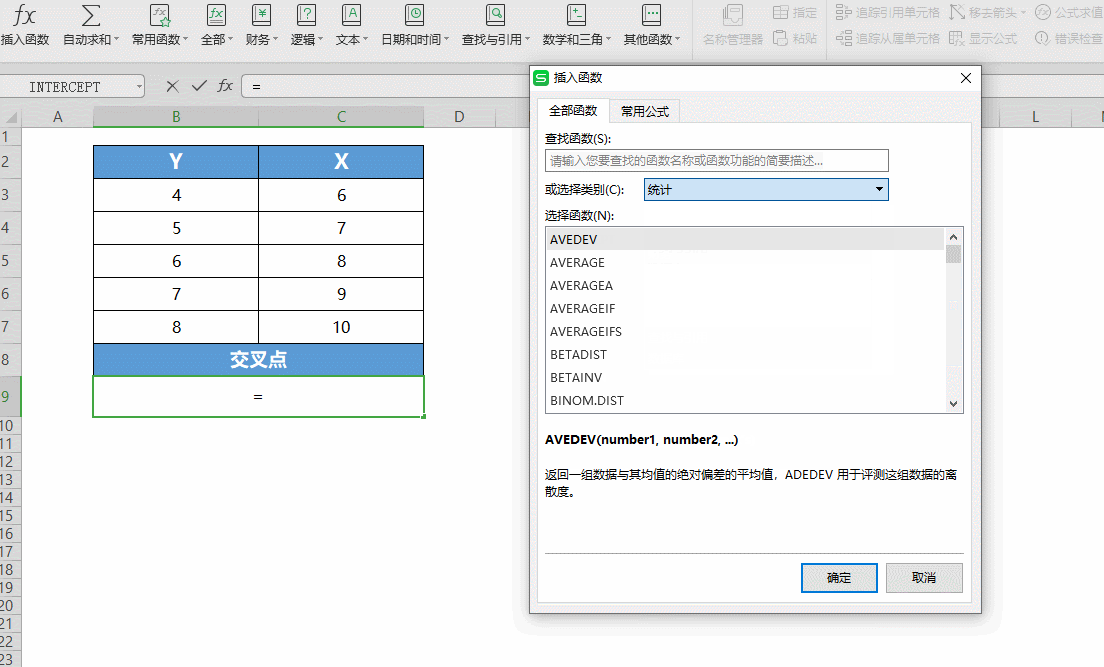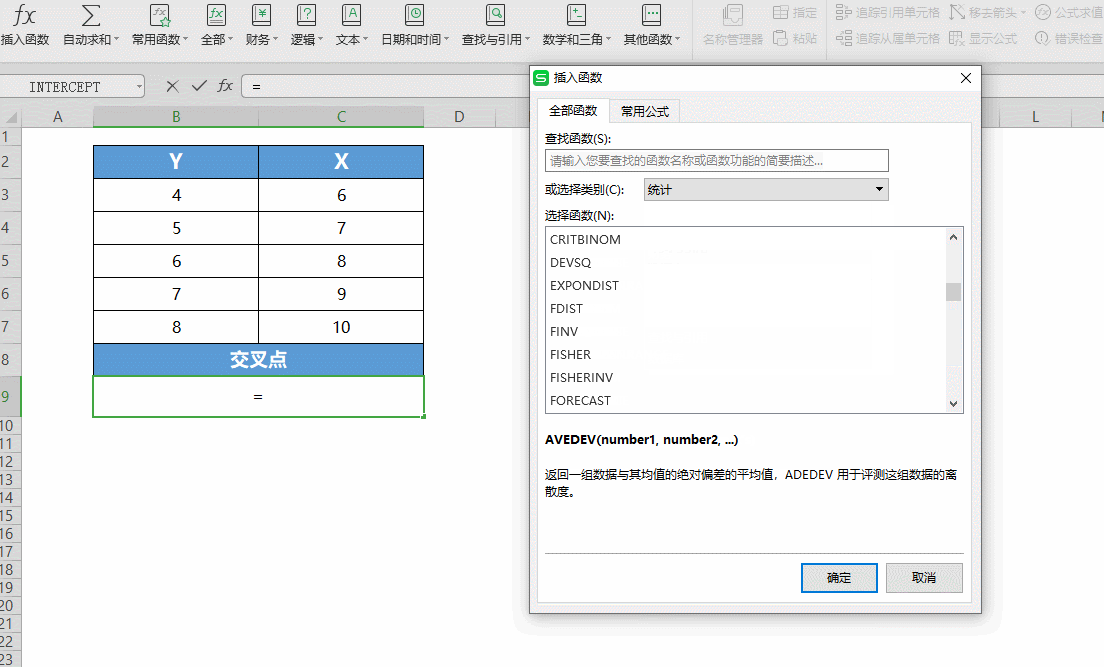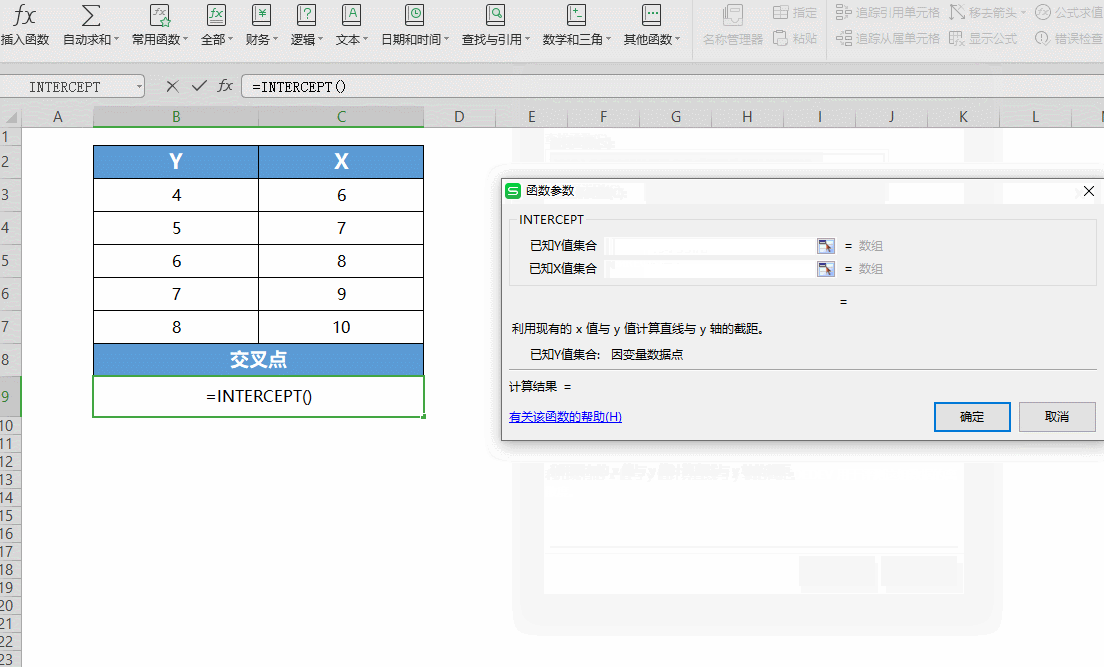
￭此时弹出对话框，共两项参数：

“已知Y轴集合”是已知的Y轴集合，输入B3：B7；

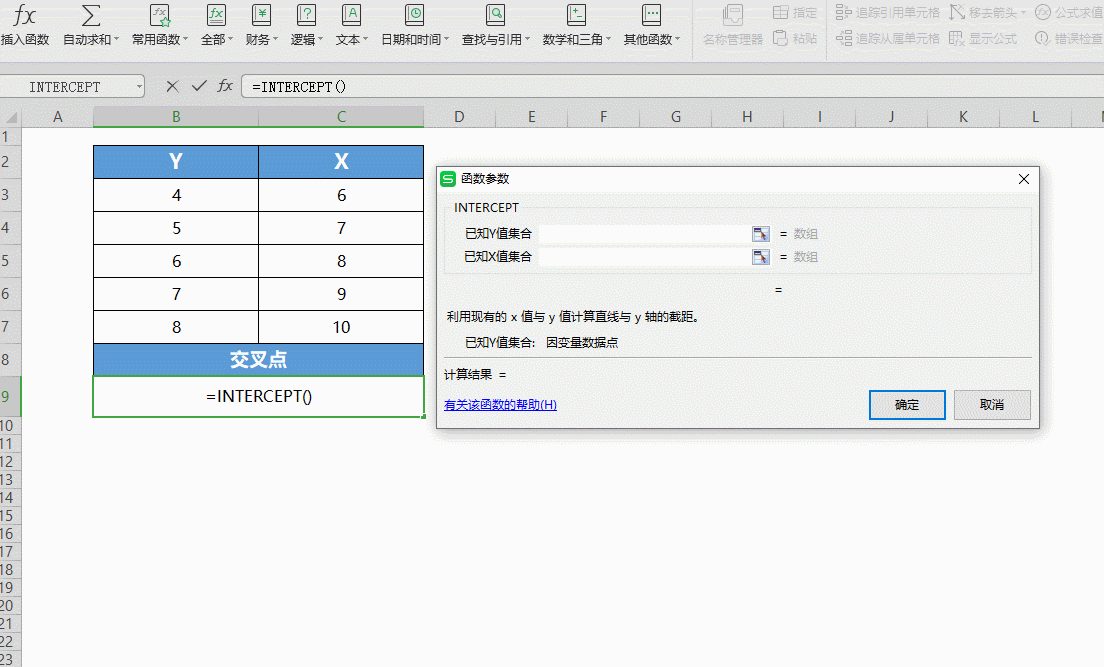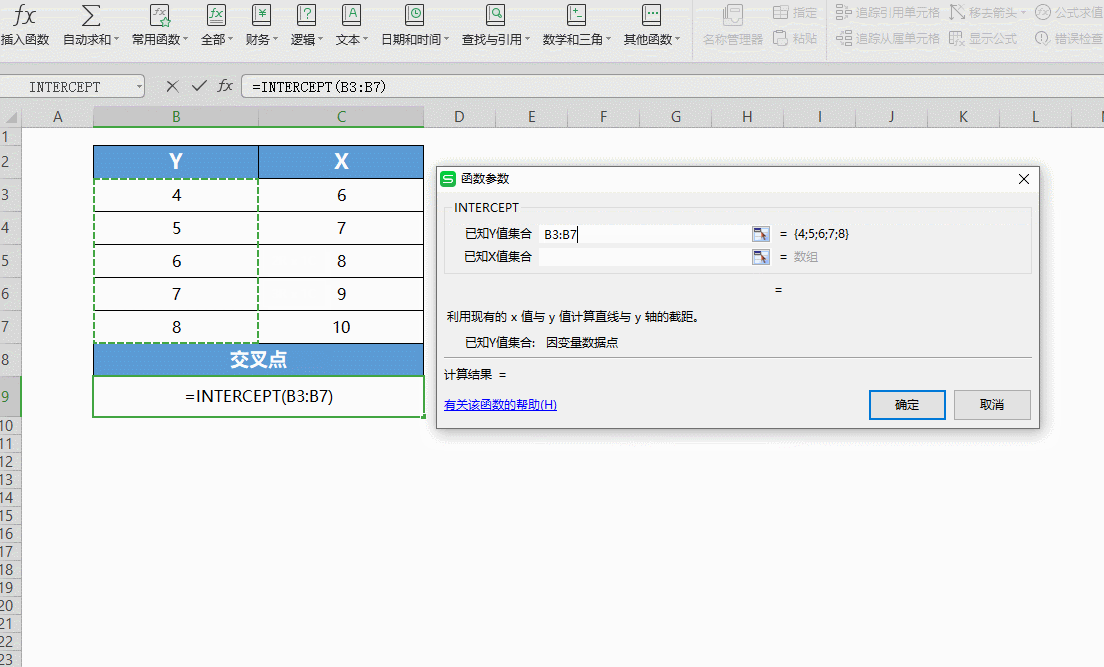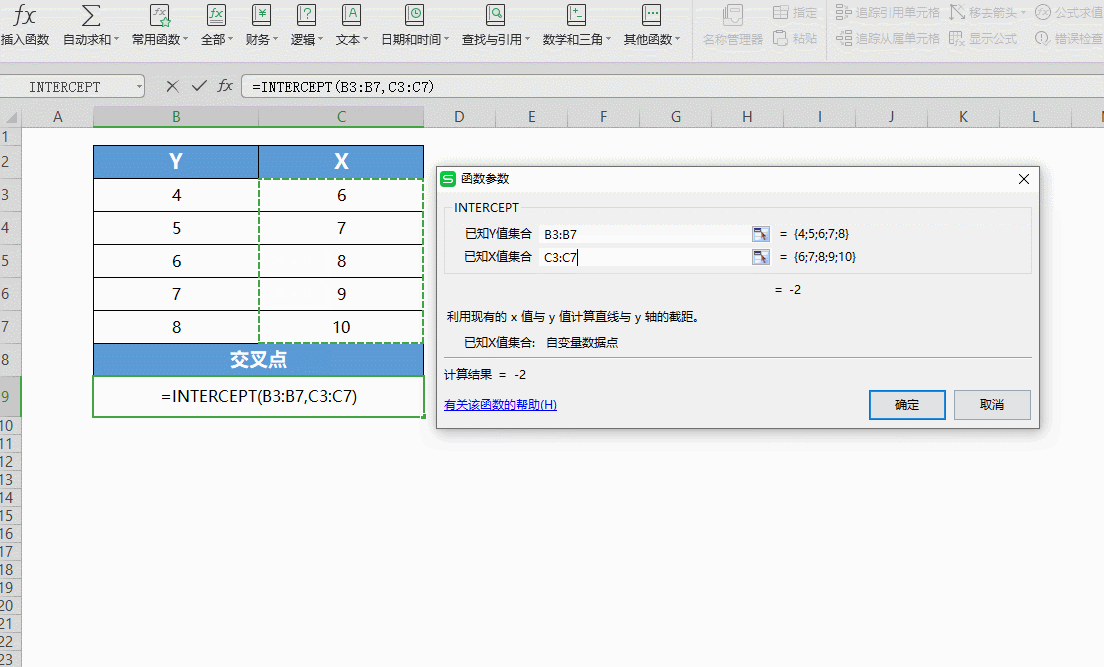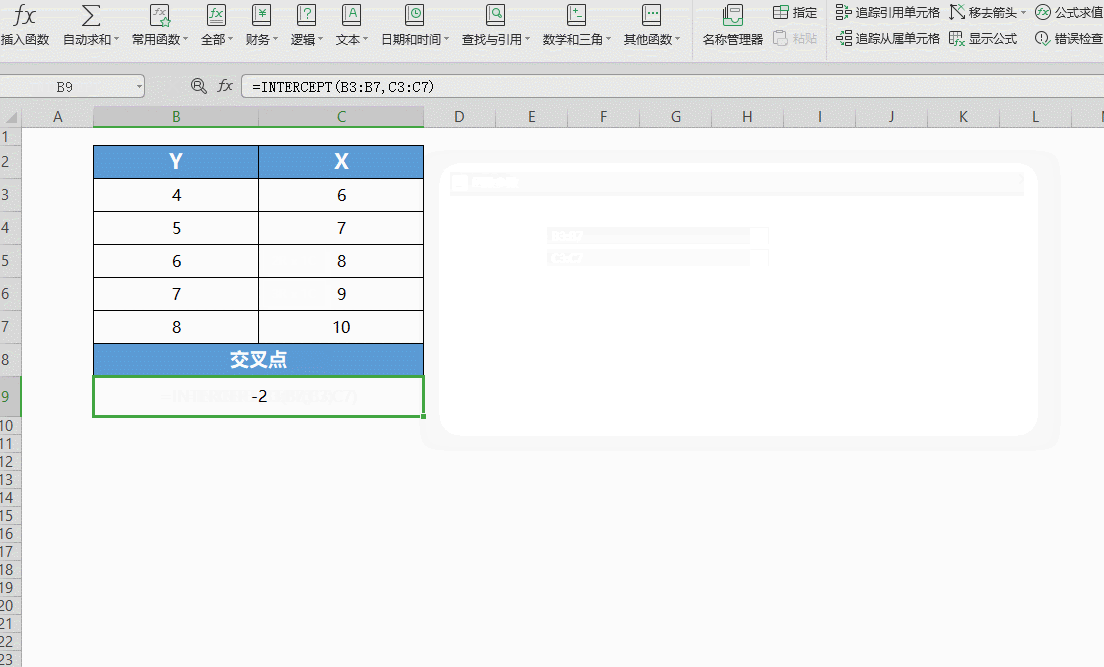
“已知X轴集合”是已知的X轴集合，输入C3：C7。

点击确定，就能得出直线与Y轴的交点。