STDEV函数：精确计算样本标准差

估算样本的标准偏差。标准偏差反映相对于平均值 (mean) 的离散程度。 

语法 
STDEV(number1,number2,...) 

Number1,number2,... 为对应于总体样本的 1 到 30 个参数。也可以不使用这种用逗号分隔参数的形式，而用单个

数组或对数组的引用。 

说明 
• 函数 STDEV 假设其参数是总体中的样本。如果数据代表全部样本总体，则应该使用函数 Stdeva 来计算标准偏差。 

• 此处标准偏差的计算使用“无偏差”或“n-1”方法。 

• 忽略逻辑值（TRUE 或 FALSE）和文本。如果不能忽略逻辑值和文本，请使用 Stdeva 工作表函数。 

当我们想知道一个班级的学生成绩分布情况差异，会用到STDEV函数，其函数作用是估算样本的标准偏差。

如果学生成绩差异小，那么这个值是很小的。如果学生成绩差异大，那么这个值就是很大的。

极限情况下，如果整个班的成绩一样时，这个值就是0。

这是某班两次模拟考试的成绩表。以此表为例，我们来实际操作一下帮助大家理解。

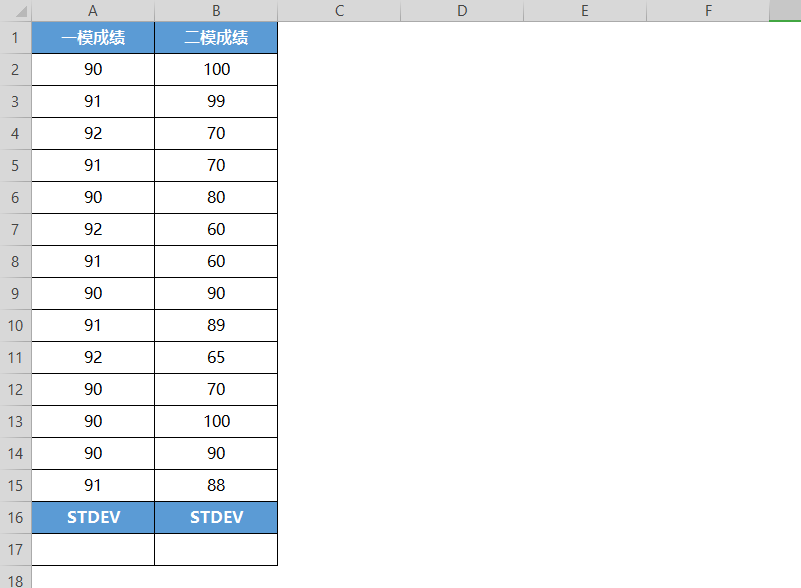
￭ 选中A17单元格，点击插入函数，在查找框中查找并选中STDEV函数，点击确定。

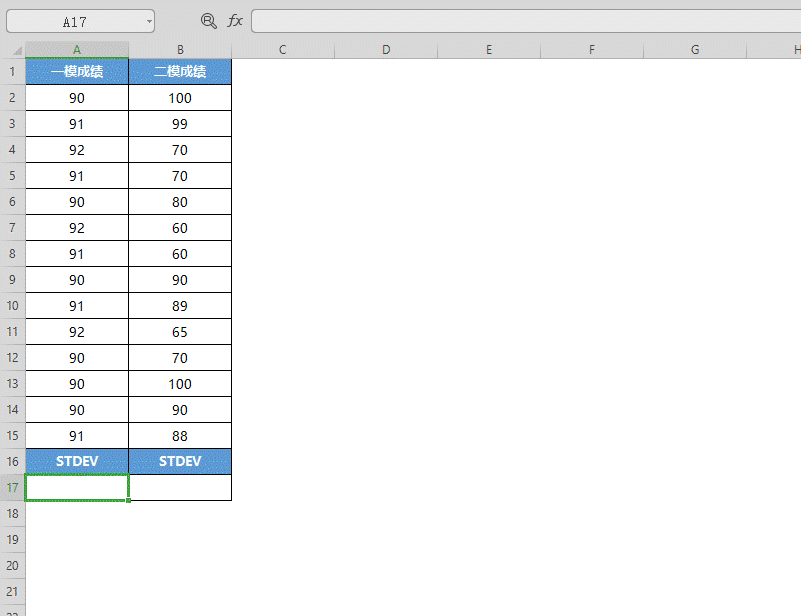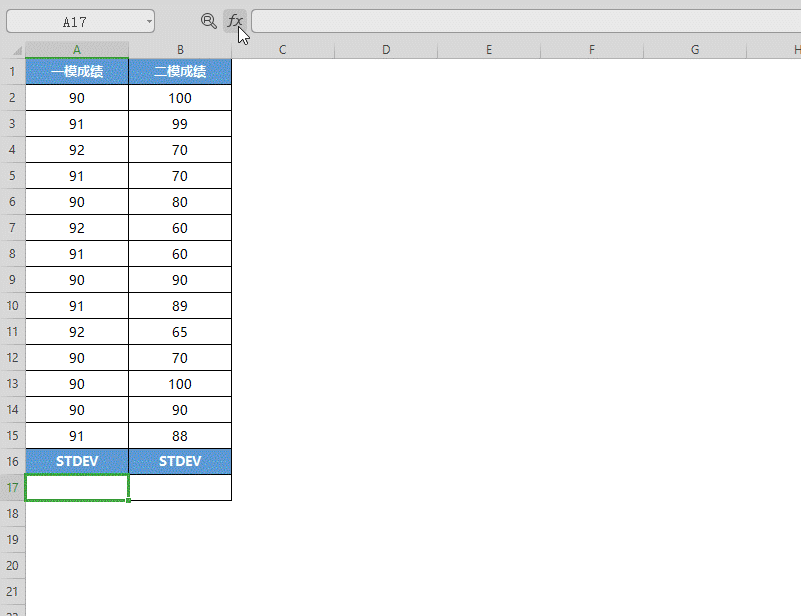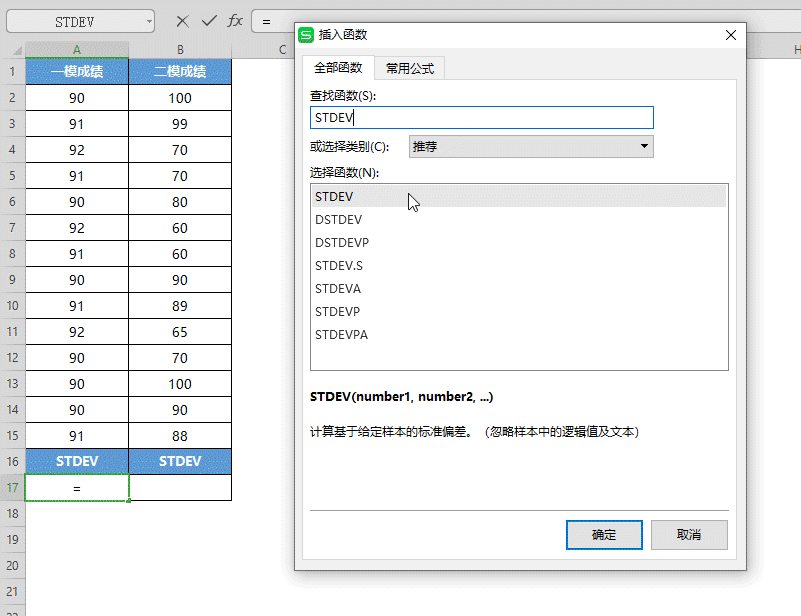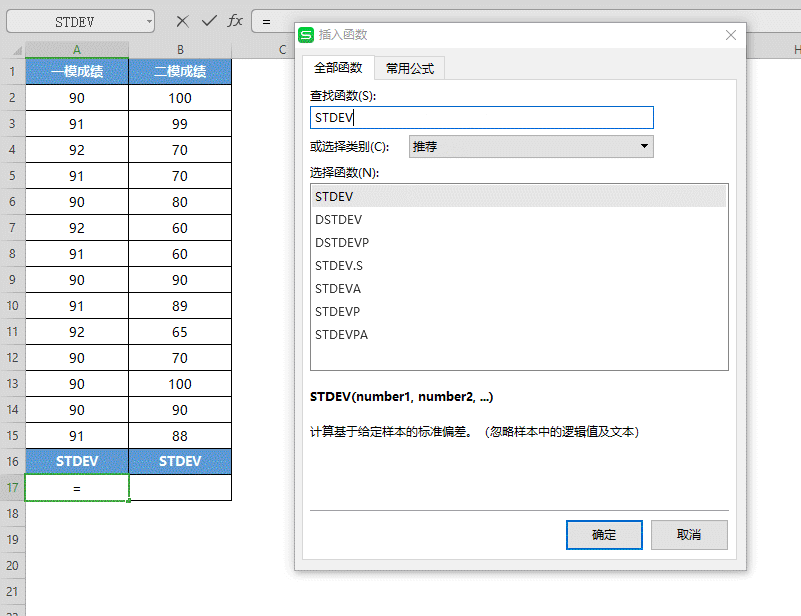
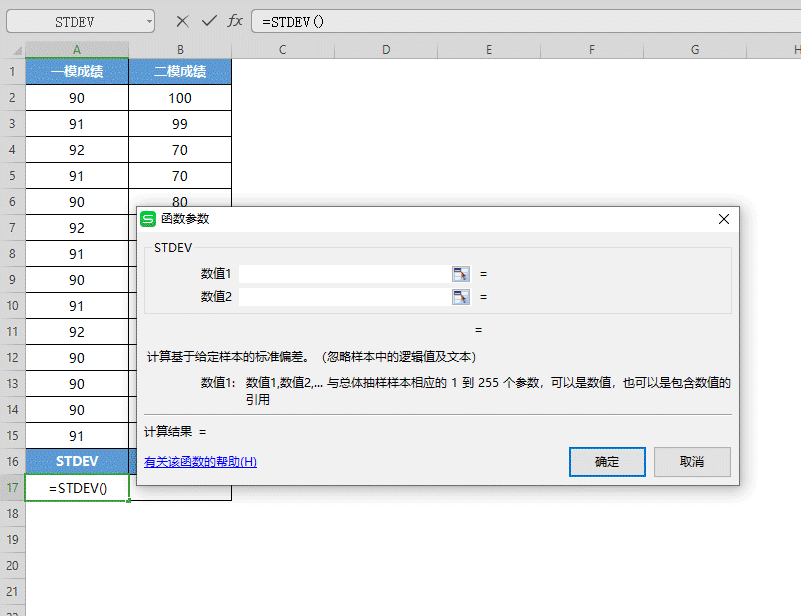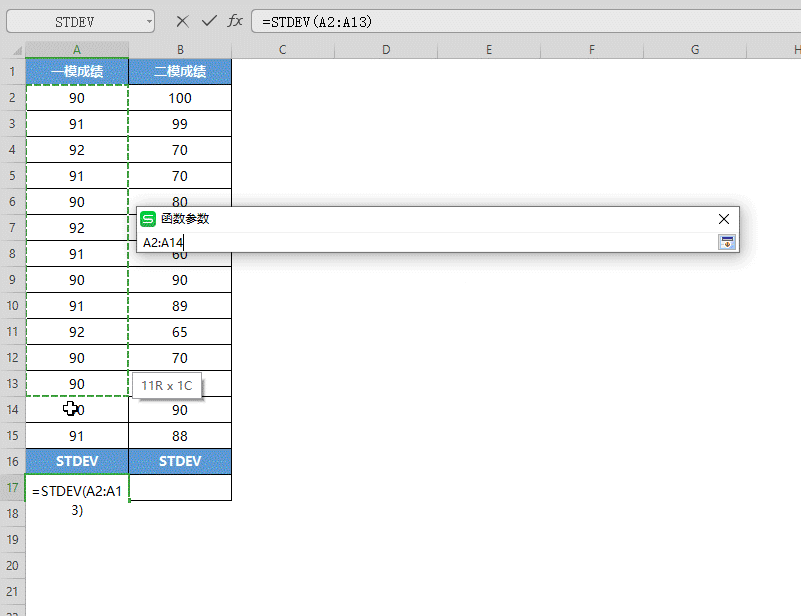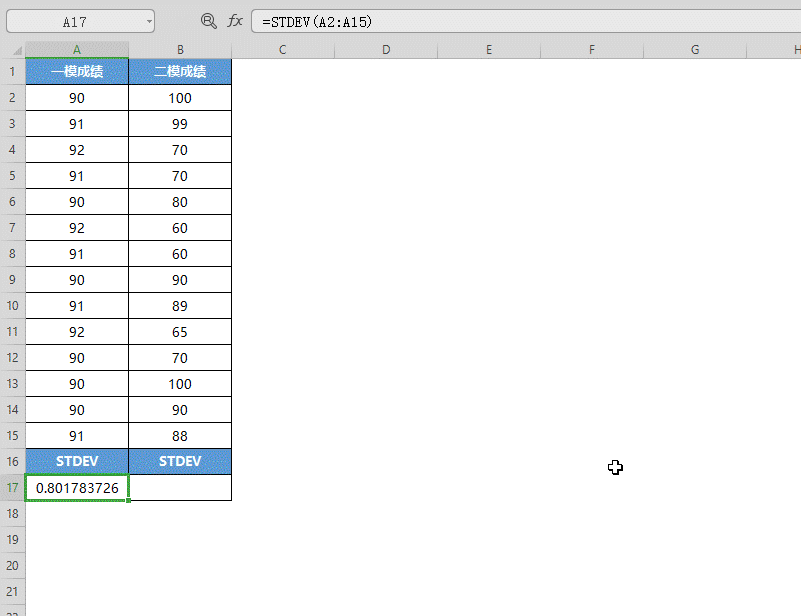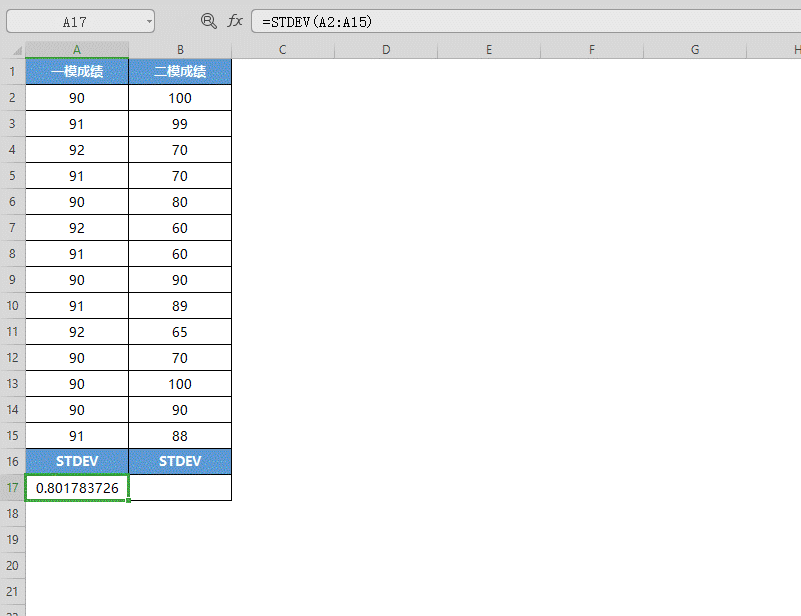
￭ 将一模成绩的数据选中填入“数值”，点击确定，即可得出数据的样本标准偏差值。

￭ 再选中B17单元格，点击插入函数，选中STDEV函数，点击确定。

将二模成绩的数据选中填入“数值”，点击确定。

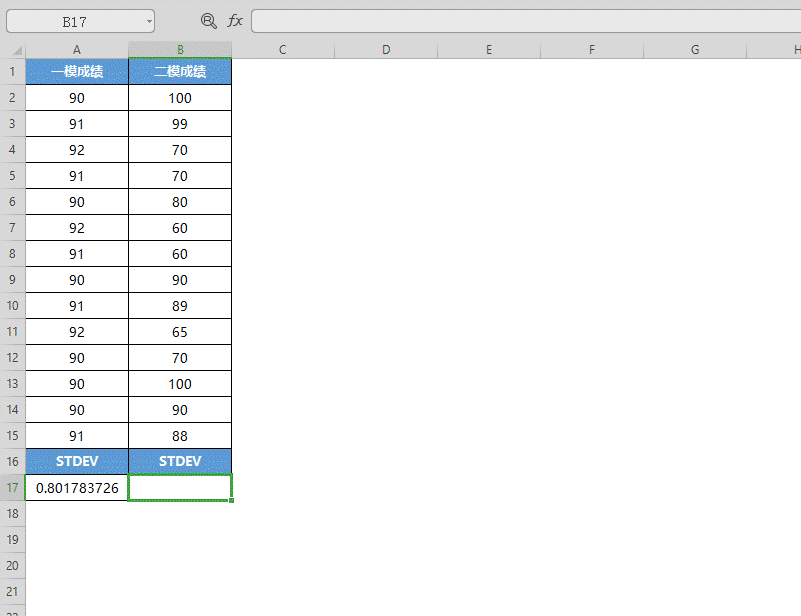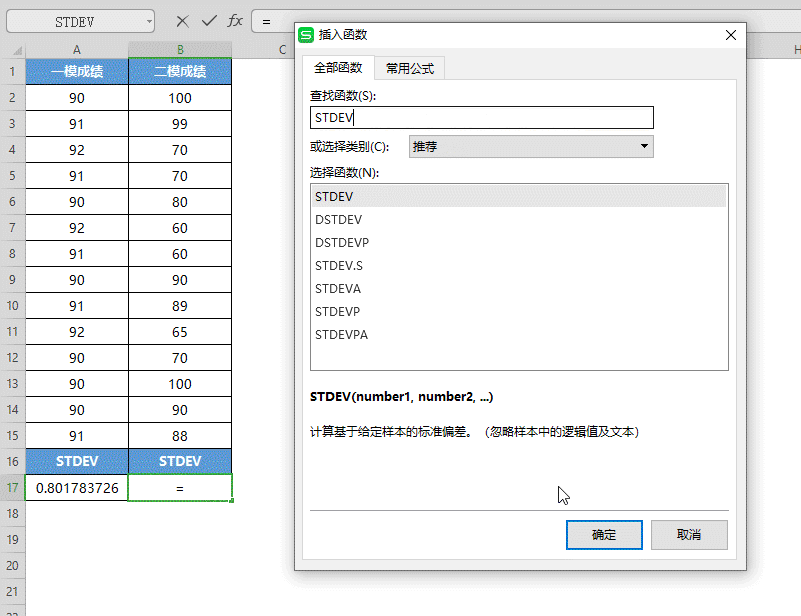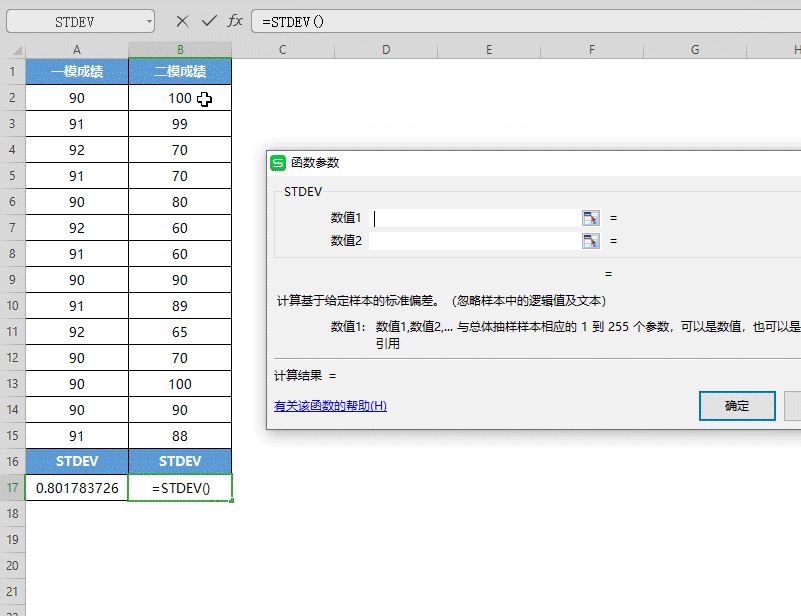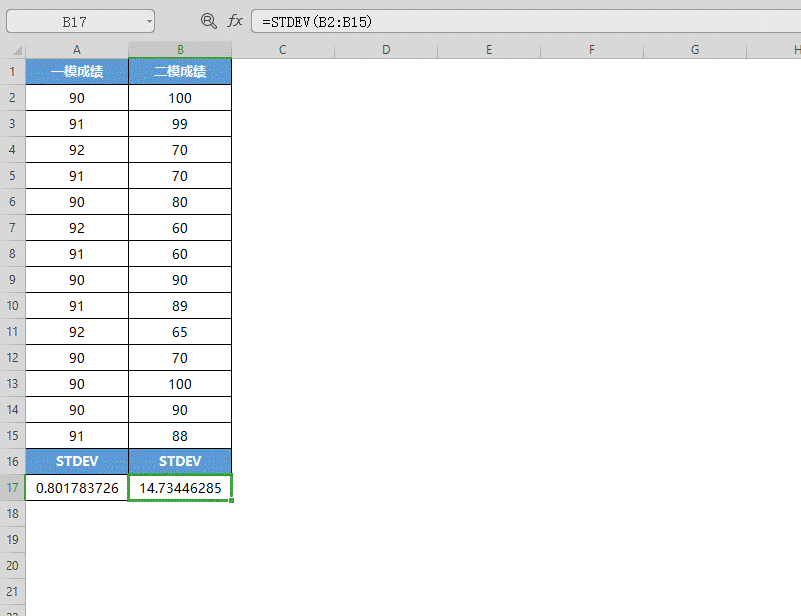
这样我们通过比较这两组数据的样本标准偏差值可以看出，一模成绩的差异较小，二模成绩的成绩差异较大。